Theory of Computation 
Section C

Construction of an FA from an RE

We can use Thompson's Construction to find out a Finite Automaton from a Regular

Expression. We will reduce the regular expression into smallest regular expressions and

converting these to NFA and finally to DFA.

Some basic RA expressions are the following:

Case 1: For a regular expression ‘a’, we can construct the following FA:

Case 2: For a regular expression ‘ab’, we can construct the following FA:

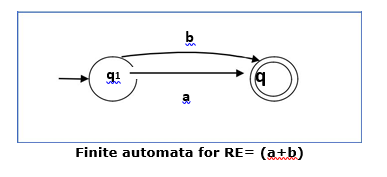
Case 3: For a regular expression (a+b), we can construct the following FA:

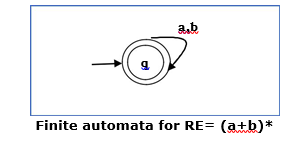
Case 4: For a regular expression (a+b)*, we can construct the following FA:

Method:

Step 1        Construct an NFA with Null moves from the given regular expression.

Step 2       Remove Null transition from the NFA and convert it into its equivalent DFA.

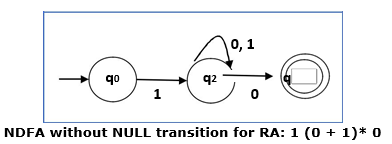
Problem Convert the following RA into its equivalent DFA:  1 (0 + 1)* 0

Solution:We will concatenate three expressions "1", "(0 + 1)*" and "0"

Now we will remove the є transitions. After we remove the є transitions from the NDFA, we get the following:

It is an NDFA corresponding to the RE: 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA