Strassen's Matrix Multiplication

 Matrix Multiplication is one of the most fundamental operation in Machine Learning and optimizing it is the key to several optimizations. In general, multipling two matrices of size N X N takes N^3 operations. Since then, we have come a long way to better and clever matrix multiplication algorithms. Volker Strassen first published his algorithm in 1969. It was the first algorithm to prove that the basic O(n^3) runtime was not optiomal.

The basic idea behind Strassen's algorithm is to split A & B into 8 submatricies and then recursively compute the submatricies of C. This strategy is called Divide and Conquer.

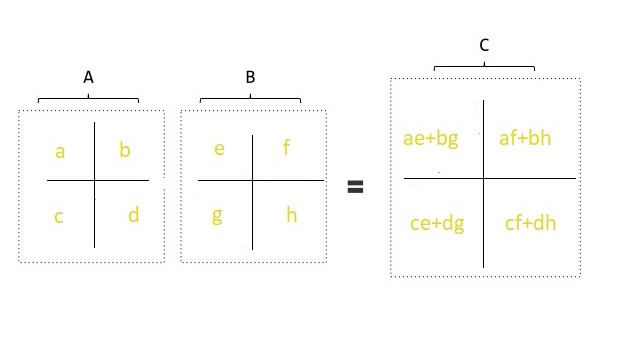
Consider the following matrices A and B:

matrix A = |a b|, matrix B = |e f|
           |c d|             |g h|

There will be 8 recursive calls:

a * e
b * g
a * f
b * h
c * e
d * g
c * f
d * h

We then use these results to compute C's submatricies.

matrix C = |ae+bg af+bh|
           |ce+dg cf+dh| 
           

The above strategy is the basic O(N^3) strategy.

Using the Master Theorem with T(n) = 8T(n/2) + O(n^2) we still get a runtime of O(n^3).

Strassen's insight was that we don't actually need 8 recursive calls to complete this process. We can finish the call with 7 recursive calls and a little bit of addition and subtraction.

Strassen's 7 calls are as follows:

a * (f - h)
(a + b) * h
(c + d) * e
d * (g - e)
(a + d) * (e + h)
(b - d) * (g + h)
(a - c) * (e + f)

Our new matrix C's new quardents

matrix C = |p5+p4-p2+p6    p1+p2   |
           |   p3+p4    p1+p5-p3-p7|