QUICK SORT ALGORITHM

Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value.

Quicksort partitions an array and then calls itself recursively twice to sort the two resulting subarrays. This algorithm is quite efficient for large-sized data sets as its average and worst-case complexity are O(nLogn) and image.png(n2), respectively.

Partition in Quick Sort

Following animated representation explains how to find the pivot value in an array.

The pivot value divides the list into two parts. And recursively, we find the pivot for each sub-lists until all lists contains only one element.

There are many different versions of quickSort that pick pivot in different ways.

1. Always pick first element as pivot.
2. Always pick last element as pivot (implemented below)
3. Pick a random element as pivot.
4. Pick median as pivot.

Quick Sort Algorithm

quickSort(array, leftmostIndex, rightmostIndex)
  if (leftmostIndex < rightmostIndex)
    pivotIndex <- partition(array,leftmostIndex, rightmostIndex)
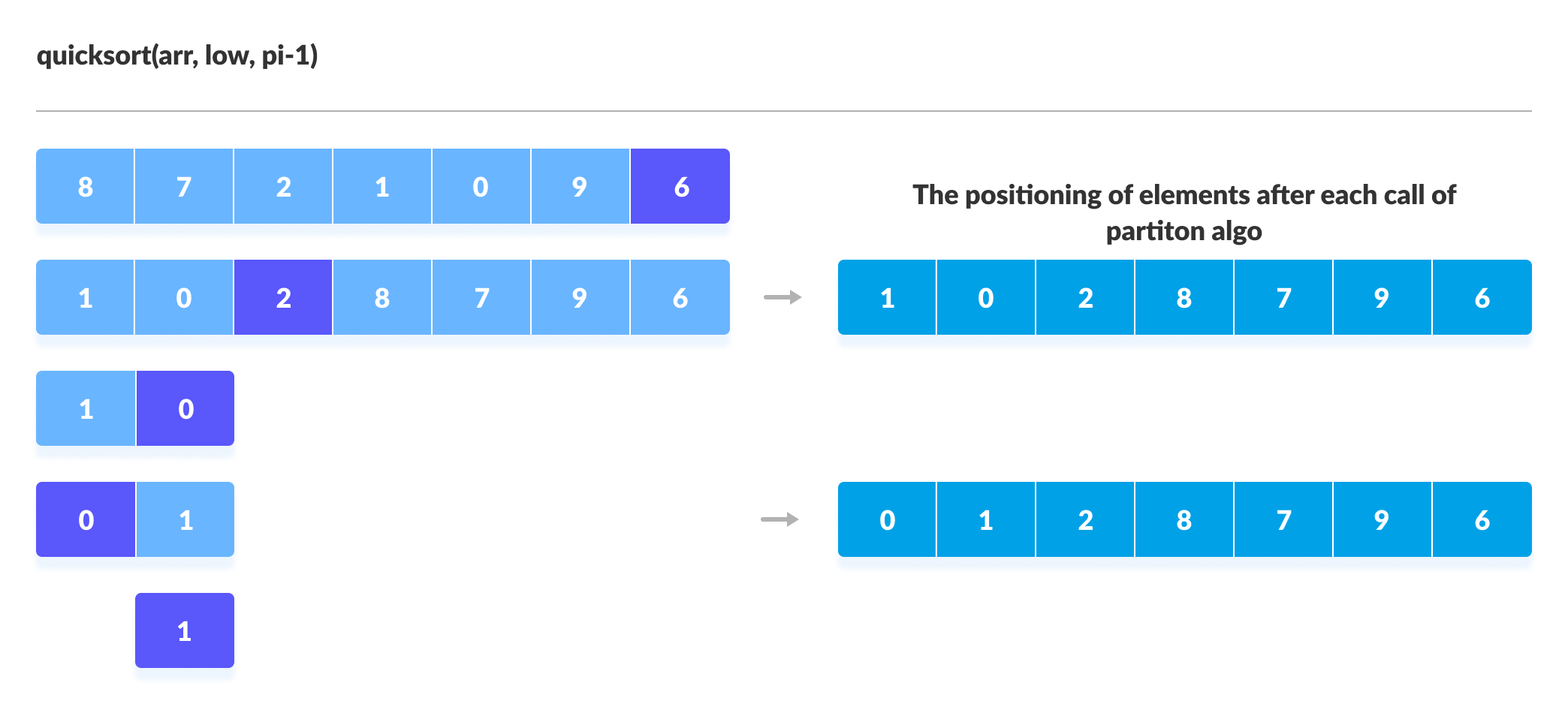
    quickSort(array, leftmostIndex, pivotIndex)
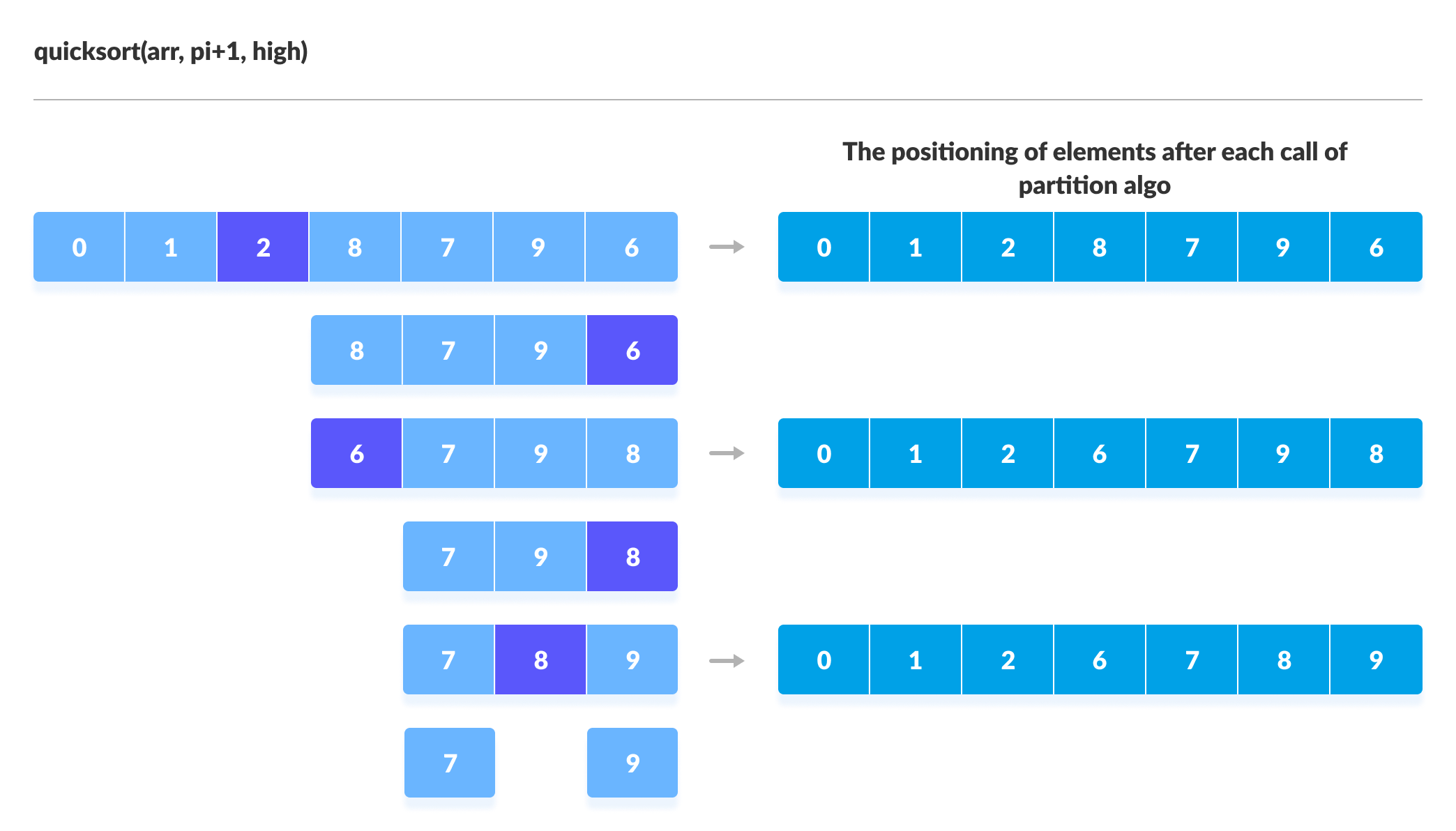
    quickSort(array, pivotIndex + 1, rightmostIndex)

partition(array, leftmostIndex, rightmostIndex)
  set rightmostIndex as pivotIndex
  storeIndex <- leftmostIndex - 1
  for i <- leftmostIndex + 1 to rightmostIndex
  if element[i] < pivotElement
    swap element[i] and element[storeIndex]
    storeIndex++
  swap pivotElement and element[storeIndex+1]
return storeIndex + 1

How QuickSort Works?

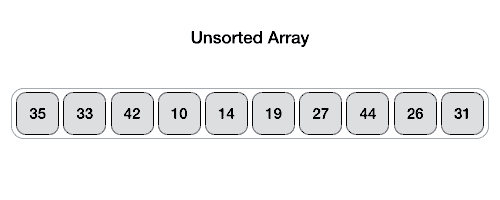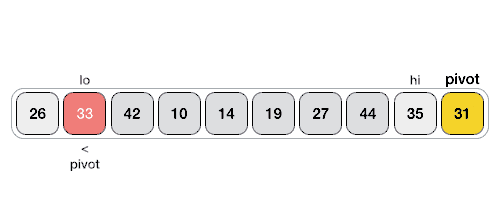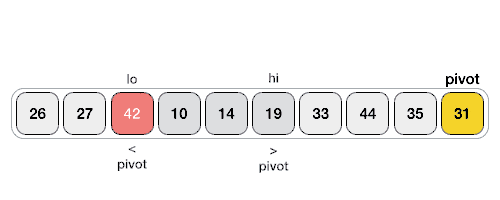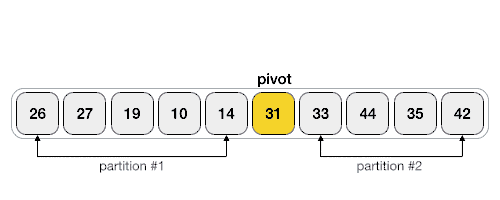
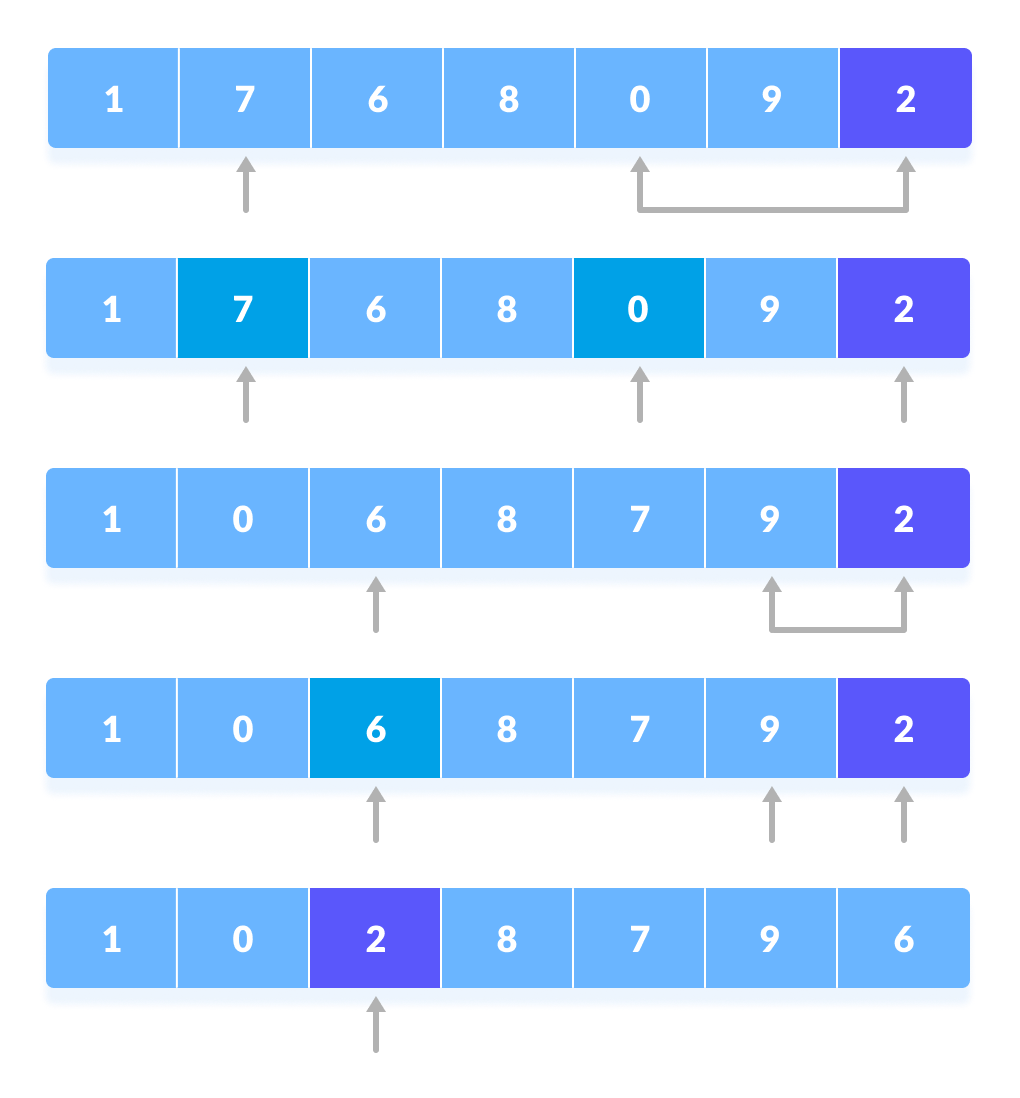
1. A pivot element is chosen from the array. You can choose any element from the array as the pivot element.
   Here, we have taken the rightmost (ie. the last element) of the array as the pivot element.

   

   Select a pivot element

2. The elements smaller than the pivot element are put on the left and the elements greater than the pivot element are put on the right.

   

   Put all the smaller elements on the left and greater on the right of pivot element

   
   The above arrangement is achieved by the following steps.
   1. A pointer is fixed at the pivot element. The pivot element is compared with the elements beginning from the first index. If the element greater than the pivot element is reached, a second pointer is set for that element.
   2. Now, the pivot element is compared with the other elements (a third pointer). If an element smaller than the pivot element is reached, the smaller element is swapped with the greater element found earlier.

      

      Comparison of pivot element with other elements

   3. The process goes on until the second last element is reached.
      Finally, the pivot element is swapped with the second pointer.

      

      Swap pivot element with the second pointer

   4. Now the left and right subparts of this pivot element are taken for further processing in the steps below.
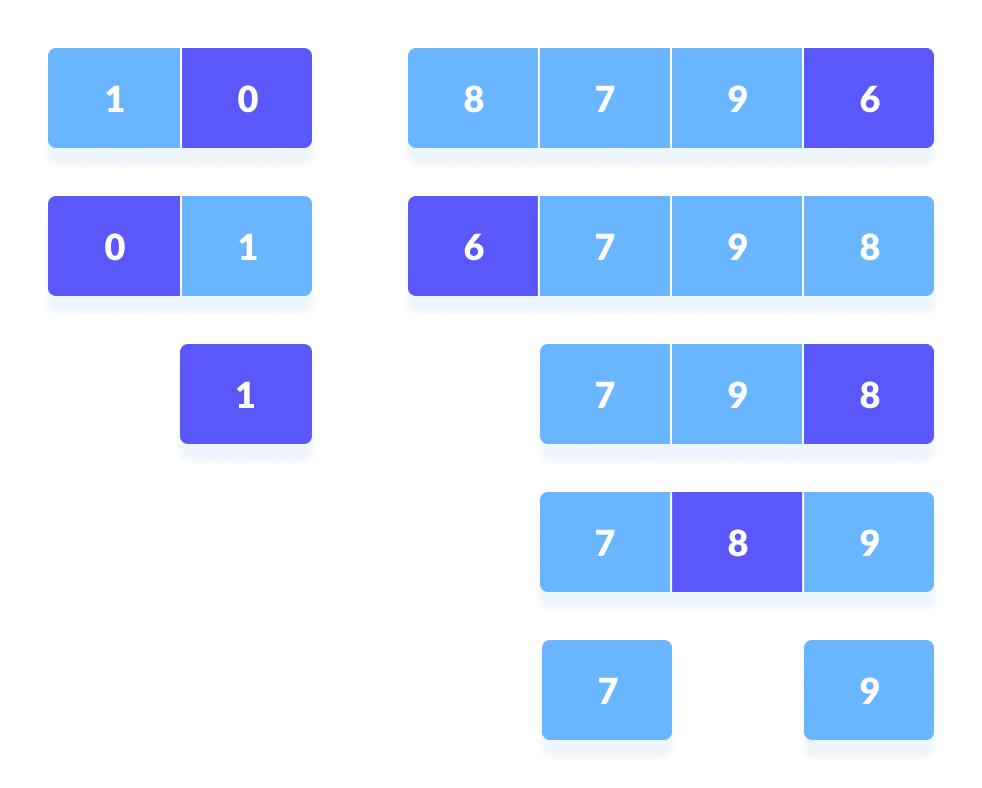
3. Pivot elements are again chosen for the left and the right sub-parts separately. Within these sub-parts, the pivot elements are placed at their right position. Then, step 2 is repeated.

   

   Select pivot element of in each half and put at correct place using recursion

4. The sub-parts are again divided into smaller sub-parts until each subpart is formed of a single element.
5. At this point, the array is already sorted.

---

Quicksort uses recursion for sorting the sub-parts.

On the basis of Divide and conquer approach, quicksort algorithm can be explained as:

• Divide
  The array is divided into subparts taking pivot as the partitioning point. The elements smaller than the pivot are placed to the left of the pivot and the elements greater than the pivot are placed to the right.
• Conquer
  The left and the right subparts are again partitioned using the by selecting pivot elements for them. This can be achieved by recursively passing the subparts into the algorithm.
• Combine
  This step does not play a significant role in quicksort. The array is already sorted at the end of the conquer step.

You can understand the working of quicksort with the help of the illustrations below.

Sorting the elements on the left of pivot using recursion

Sorting the elements on the right of pivot using recursion